A Differentially-Private Decentralized Machine Learning Framework

​ Master’s Thesis 2019 - ETH/EPFL - Alexandre Connat

Introduction - Outline

In this article, I will try to give the reader a high overview of my Master Thesis: “A Differentially-Private Decentralized Machine Learning Framework”, realized in 2019 at the Distributed Systems Group (DSG), ETH Zürich.

There are three important part in this somewhat complicated title, that I will try to break down and explain in simpler terms:

• First, we will describe what “Decentralized Machine Learning” means, and why is it currently such a “hot” topic.
• Second, we will discuss the notion of “Differential Privacy", and explain why it is important and relevant to us.
• Finally, we will talk about how we combined both of these things in one system, show how our approach compares to existing methods, and consider how it can be further improved.

Decentralized Machine Learning

I do not think I have to re-emphasize how important Machine Learning (or ML for short) has become in today’s society. It is used in virtually every field, or any sector of the industry: supply chain, medicine, finance, … you name it!

Of course, to train a Machine Learning model, you need… some data! And the more precise this data is, the more accurate your model will be.

However, in certain fields, like medicine for instance, this data could be highly sensitive. Imagine a dataset of people suffering from Cancer, used to train medical predictive models. But you can also think of private industrial processes, or financial figures, that you would not want to see out there, in the wild!

And finally, in the case of these big Technology companies, like Facebook or Google: you are the product, and you are also the data creator. Facebook might want to train their speech recognition system on your voice messages, but… these messages are inherently private, and first and foremost, belong to you.

In parallel, as we see today, there is a big incentive to decentralize the Machine Learning training process. And here, by “decentralizing” I do not mean run ML algorithms on different nodes, but rather having the training data taken away from the computation source.

There are actually two big incentives to do so:

• The first one being when companies do not posess the in-house ressources (or even knowledge) to run their own analytics on their data. They tend to assign this task to a cloud providers (like Amazon, Microsoft, Google, …) to run these expensive ML algorithm for them. $\rightarrow$ This is a slightly related but a separated concern from ours, and it is often refered in the litterature as “Outsourced Computation".
• The second one is the one we are most interested in: when you want to run analytics on data that is spread across several different locations (i.e, machines, devices). The problem becomes particularly interesting when we cannot trust any entity to centrally aggregate all that data in one place. $\rightarrow$ This problem of computing something with distant agents that do not neccesarily trust each others is refered as “Secure Computation".

This last problem is exactly the one we discussed above, about big tech companies. Say you are willing to let Facebook train their algorithms on your voice messages. Still, you hope there is a way for them to extract the knowledge from these messages, without learning anything in particular that could directly identify you. And above all, you do not want to send them directly these messages! You don’t trust them. This would completely violate your privacy.

Nevertheless, this is currently what is happening, as the scandals from these past weeks show us, despite Mark’s reassuring statements during his last keynote on April 11:
11/04/2019 - Amazon admits employees listen to Alexa conversations / Why does it matter
13/08/2019 - Facebook admits contractors listened to users’ recordings without their knowledge
15/08/2019 - Microsoft admits humans can listen to Skype, Cortana audio

This is the first of two concerns in Decentralized Machine Learning, that I will call “input privacy” (or input secrecy). The second one being the “differential privacy” of the model, that we will dicuss in more details later on.

Note that here, “input” has to be taken in the broader sense of “whatever enters into the ML system", and does not necessarily mean the raw data (your raw voice message, in the above example). For instance, if the raw data is a simple integer $x$, the input to the ML system could be a function $h(x)$ which computes $x \ \text{mod} \ 2$. Here, the evil server observing the input just sees a “0” or “1”, but it can still know the parity of $x$, and that is already a leakage, that combined with additional information might lead to a real compromision of a user’s privacy.

Protecting not only the raw input itself, but also everything that have been infered from it, is of paramount importance. For instance, as we will see later in the article, in Distributed Stochastic Gradient Descent, the input to the DML system would be a gradient vector. But as we will see afterwards, even a simple gradient could leak a lot of information on the data it has been computed upon. In some very simple case, you can imagine the gradient as just a scaled version of the raw data.

• What I will call input privacy is when you want to protect the secrecy or at least the privacy of the input itself, being a raw training data sample or any information you can infer about it from this input.

• Differential privacy, on the other hand, looks at the ML system as a whole, and cares about protecting the privacy of the training set, used to train the model. In other words, we want to address the question: “Just by looking at my model as a white-box, or even as a black-box, how much can an adversary learn about individual data samples it has been trained on?”
  … and Guess what? A lot of things!

  White box means here that the adversary can inspect internal parameters of the model. In a black box scenario, the ML system is reduced to a simple query mechanism: you input a sample, it outputs a prediction.

This leads us to talk about the three most common misconceptions people tend to have about Machine Learning:

• That ML is some kind of magic box in which we put all our data into, and it will solve all the world’s biggest problems.

• That ML models makes completely reasonable, fair, and undiscutable decisions.

• That it is absolutely safe to use ML in any situation, on any data.

  On this last point, I’m not so much talking about the reliability or “robustness” of a model (broken by things like evasion attacks or dataset poisoning), but more of the privacy guarantees of a trained model itself.

The first two of these misconceptions are being addressed by the Machine Learning community by respectively talking about the intricacies of fine-tuning to the general public, and pushing forward research in areas like “model interpretability” which try to circumvent the bias models may have when trained on biased datasets. Finally this “robustness” problem has been addressed by things like adversarial training, explained and theorisized as soon as in 2014, but relates more to the Security concerns of Machine Learning (and might even harm its privacy aspects).

However, the machine learning community seems to remain desperately blind to the last point, which considers the privacy risks of using machine learning on sensitive data.

Indeed, there has been a lot of evidences in the litterature (M.Fredrikson et al., R.Shokri et al.) that a trained model, even released as a black-box query system, leaks a lot of information about the data it has been trained on. This is particularly true with big models such as deep neural networks, that tend more to memorize the whole dataset instead of learning general patterns in the data distribution.

An adversary can leverage two types of attacks against a machine learning model:

• Membership inference attacks, where the adversary learns whether or not a particular sample was part of the training dataset.
• Model inversion attack, where the adversary reverse-engineers the model from its internal parameters leading to partial or full reconstruction of data samples. That’s how for instance some researchers have managed to extract and reconstruct credit cards and social security numbers from a model trained on scanned emails. Or to recover some faces from the dataset used to train a facial recognition algorithm, just querying it and using information from the confidence score vectors.

In the absolute worst-case scenario possible, publishing a trained model looks a bit like publishing the training dataset itself; as some machine learning models behave a lot more like a lookup table, than a general intelligence that can recognize and identify patterns.

You might argue, in some less “extreme” cases than scanned emails (e.g: medical records of patients), even having access to the whole dataset is not such a big deal, right? After all, it is anonymized. All you can look at is a bunch of meaningless numbers!

If you really think that, don’t worry, you just need a big recap class on Privacy research. As the years taught us, Anonymization simply does not work.

In Privacy research, we generally make no assumptions about the background knowledge of an adversary. Hence, by looking at the data itself, he might be able to infer a lot more things that you think.

There have been techniques developped and used in Privacy-Preserving Information Publishing to reduce the granularity of data, like k-anonimity, k-map, l-diversity, t-closeness, $\delta$-presence, etc… and I want to talk to you about Differential Privacy, which is a powerful defition that allows us to reason in the general case, without any assumptions, and formally quantify the amount of privacy leakage with mathematical rigour.

Differential Privacy

Informally, a data process (say a machine learning algorithm, or a simpler computation on the data) is said to be differentially private if its output run over 2 neighboring datasets is approximatively the same.

We call neighbours datasets, two datasets only differing by one sample

This is what captured by this definition: $$ \mathbb{P}[A(D_1)=O] \le e^\varepsilon\cdot\mathbb{P}[A(D_2)=O] $$

Of course, we want epsilon to be as small as possible

Imagine you have a database $D_1$ containing the salaries of $n$ people, from which you remove user “Joe” to obtain this second database $D_2$ of size $n-1$. We will define our algorithm “$A$” as a simple averaging operation. If our algorithm is differentially-private, it should respect this formula. In other terms, it should output approximately the same value on D1, or on D2, such that it would be undistinguishable for an adversary whether Joe was or not in the dataset, just by looking at this value.

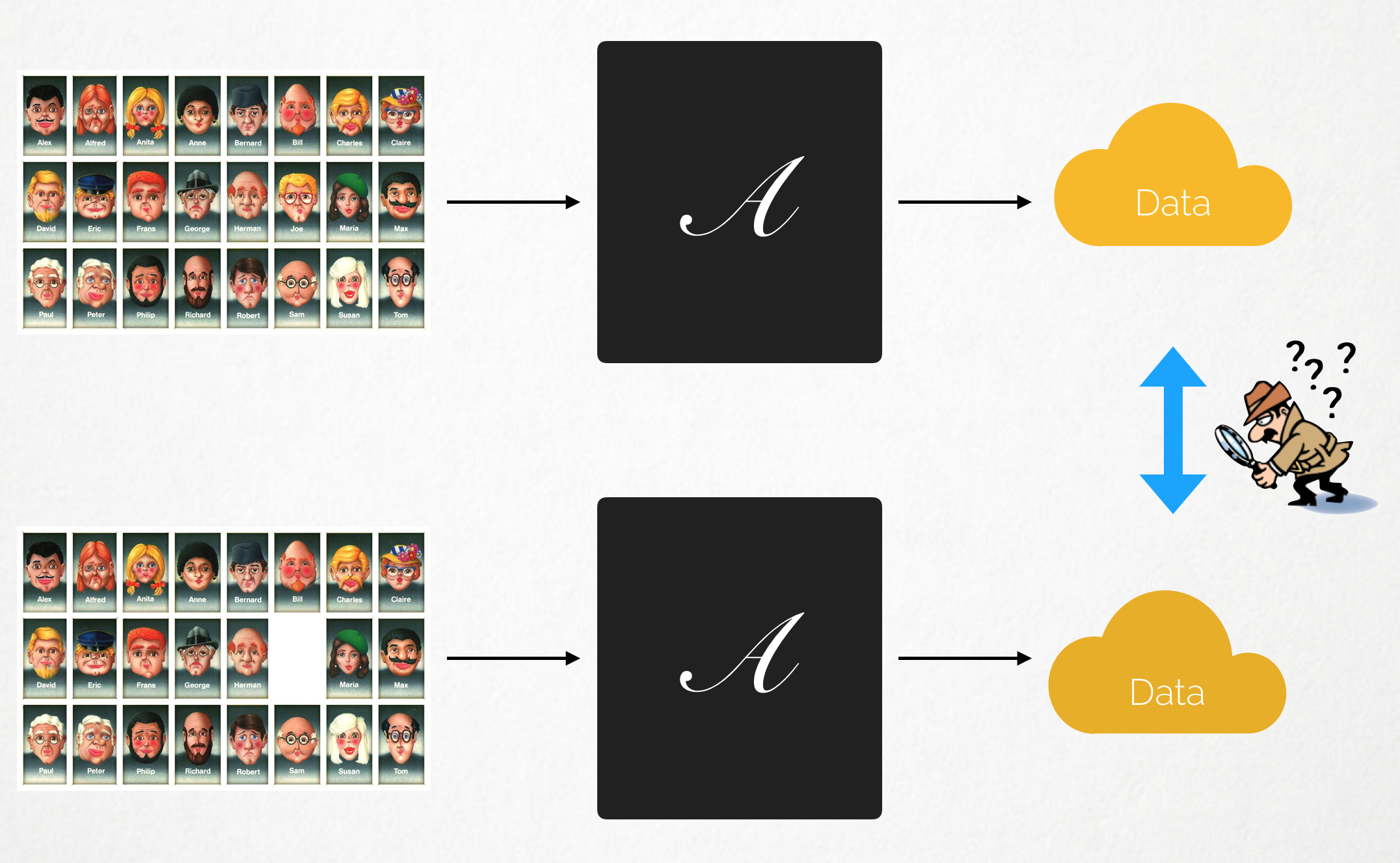
As you may imagine, this requires the algorithm to introduce some randomness (i.e some noise) in the computation process.

Looking at the formula, from a Bayesian perspective, this “$\epsilon$” represents the “amount of a posteriori knowledge” that an attacker gains, after looking at the output of $A$.

For instance, let’s say that an attacker was 50% certain that a target was in the dataset (i.e he has no clue), a $\epsilon$ of 1.1 would mean that by observing the output of $A$, he can “update” his suspicion to up to 75%.

As the noise is inversely proportional to $\epsilon$, the bigger the noise, and the smaller $\epsilon$ is, hence increasing the uncertainty of an adversary and leading to good privacy guarantees. However, too much noise would completely destroy the utility of the algorithm.

Understanding this definition from an intuitive perspective will help us fully comprehend the rest of the article. A differentially-private ML training algorithm is no different from our example above of a differentially-private “salary averaging system”. The only difference is what we call $A$ here is the method used to train a ML model. In this case, the output is the trained model (or rather the set $O$ of possible models) itself. I think this is what brings a lot of confusion. To me, it never made sense to say “this ML algo is DP”. But I would rather say “this ML algorithm has been trained in a differentially-private manner”.

Differentially Private Machine Learning

I want to motivate the rest of the article by a simple example taken from the Threat Intelligence world: Every day, companies receive thousands of malwares, and use anti-viruses and tools to detect and categorize these malwares. However, hackers are always more clever and now easily manage to evade those rule-based detection mechanisms. This led the security industry to design machine learning-based tools and rely on Threat Intelligence to classify new malwares.

Each company typically has to adapt such a system to their infrastructure, by training these ML systems on large corpuses of evidences that they gathered. This data could be highly sensitive as it could include hostnames, IP addresses, memory dumps, parts of the filesystem, …

However, companies (especially medium-size ones) generally cannot gather a huge amount of intelligence by themselves, and would benefit from other companies knowledge and insights. In his TED Talk, Caleb Barlow, an ex-vice president of IBM security, compares cyberattacks to pandemics and show we should respond in the same way, and incentivize companies to openly share information about their breaches and infections.

[…] Let’s think of the response we see to a healthcare pandemic: SARS, Ebola, bird flu, Zika. What is the top priority? It’s knowing who is infected and how the disease is spreading. Now, governments, private institutions, hospitals, physicians – everyone responds openly and quickly. This is a collective and altruistic effort to stop the spread in its tracks and to inform anyone not infected how to protect or inoculate themselves.

Unfortunately, this is not at all what we see in response to a cyber attack. Organizations are far more likely to keep information on that attack to themselves. Why? Because they’re worried about competitive advantage, litigation or regulation. We need to effectively democratize threat intelligence data. We need to get all of these organizations to open up and share what is in their private arsenal of information. […]

This idealistic view might become reality if we can get rid of the fear companies would have to openly share potentially sensitive information. To my opinion, this fear is even more intense as the one we might have from Facebook reading personal conversations of users, as this one is specifically business- and profit-oriented.

So let’s take this example of a malware classifier. We will consider a black-box machine learning algorithm (you might think of a deep neural network, or any kind of fancy architecture of your choice) which takes as input some suspicious files along with their context (extracted Indices Of Compromise (IOCs) and identified Tactics, Techniques and Procedures (TTPs)) and returns the category of the malware, one among these 10 classes:

That’s where we introduce the idea of Knowledge Transfer.
Remember, companies do not want to share their private information, but just the necessary knowledge one can extract from it to help train a global model, without taking the risking that the latter remembers any information that could be used to identify any of their data samples in particular.

The idea goes as follows:

1. Each company trains a local model on their own private dataset. We call these models “teacher models”, or simply “teachers”.

   Each of those models could have a different architecture, as long as they remain 10-classes classifiers as in the example above. ***NB:* We assume (and this is a primordial assumption) that all companies’ datasets are disjoint. In practice, one can check quite efficiently that the intersection between any two pairs of datasets is empty using Private Set Intersection protocols.

2. Once all of these teacher models have been sufficiently trained, we ask them to predict on public data samples. Their prediction is called a “vote”, and it only consists in the class that their model predicted.

   NB: We will call “prediction” the output of a teacher model, and “vote” will refer to what the client send to the aggregator.

3. We collect all these votes and aggregate them centrally, to perform some kind of “noisy majority voting": The class with the most votes is selected, and this public data sample is labeled accordingly.

   Why noisy? Remember, we want to make our decision process differentially private, hence we put some noise on top of the votes, in order to mask their true count, and hide as much as possible individual contributions (see blue/orange histograms below).

4. All these public data samples, alongside with their assigned labels, will constitute the training set of a final classifier, called a “student model”. This last model can be formally proven to be differentially private, and hence could be safely released publicly, even as a white-box model.

This technique is refered as “Private Aggregation of Teacher Ensembles” and has been first introduced by Nicolas Papernot and a team from Google Brain. The method provides an elegant way to guarantee the differential privacy of the student model, trained to copy the input-to-output mapping these multiple teacher models. And because no two teachers are trained on the same examples; whenever they agree on what the output should be, we know that they agree because of a general pattern, rather than because they memorized something about their own training examples. Hence, it is safe to copy that knowledge into the Student.

As a parenthesis: The Confident GN-MAX protocol

In an iteration to the PATE paper, Papernot devised a way to avoid the problem of misclassification in the case when teachers do not agree. We can decide not to asign any label to a data sample if there is not a large enough consensus in teachers’ predictions around a particular class.

Starting from the observation that the more confident teachers are, the more we can inject noise without risking to perturb the distribution too much (hence overthrowing the candidate with most votes), it allows us to tighten our privacy bounds, by injecting more noise when teachers agree. It is one of these rare cases where privacy and utility are compatible, and not conflicting each others.

The CGNMAX procedure goes as follow:

• Let $v$ be the final aggregated votes vector (the blue histogram below). We take its maximum value, and noise it with gaussian noise with a high variance $\sigma_1$.
• If the obtained value is not passed above a certain threshold $T$ that we can defined as “60% of the teachers” for instance, it means there was probably no clear consensus among the teachers. Hence, we do not assign any label to this public sample.
• Otherwise, we reiterate the noising mechanism: We noised the aggregated vote vector $v$ with a gaussian noise with smaller variance $\sigma_2$ (giving a more precise estimate on the true votes distribution), and select as our label the argmax of the obtained vector.

We designed our two protocols below to perform this “consensus check” but for the sake of simplicity, we will not talk about it in this article.

We might now think we can tick our two boxes:

• Differential privacy, … Check! The final model is differentially private, and an adversary will hardly find evidences of any individual data samples just by inspecting it.

• Input privacy, … Wait a minute..! Even though we do not send the raw data sample to a server, there is still a central entity collecting and noisily aggregating the votes from every teacher. It means that this entity leans any individual vote. To express it the same way as above, each teacher does not send $x$ but some $h(x)$ to the server, $h$ representing here their ML model. An adversary might infer a lot of information from that vote alone!

  In our example of malware classifier, let’s assume an adversarial aggregator (server) has knowledge that the model of Company3 never predicts category “Trojan”, except if the company had trained it on some malwares containing WannaCry payloads. In that case, if the aggregator sees Company3 predicts “Trojan”, it can be pretty certain the company was previously affected by the nasty ransomware.

  Not only the individual votes, we really want to protect the whole distribution of votes. With sufficient background knowledge, an adversary might be able to deduce something from the blue histogram below, alone. It can for instance rely on extreme cases like classes that have zero votes, or exactly one vote.

If we consider this voting process itself as our differential privacy mechanism, this problem looks a bit like the Local vs. Global Differential Privacy problem, which put into perspective two paradigms:

• In the Global DP paradigm, a central aggregator collect data about individuals. Each of these individuals send their data to the aggregator without noise, and the latter is responsible to transform that data using a differentially private mechanise, i.e injecting the noise itself.
• In the Local DP paradigm, the aggregator no longer has access to the “true” data, as each individual is reponsible to noise their data before sending it for aggregation.

The local differential privacy model has the advantage of getting rid of all trust we must have in the aggregator. However, since each individial needs to inject enough noise in their data to hide it properly from the aggregator, the aggregate result then become less accurate than in the global model where the differentially private mechanism is only applied once, and requires a lot less noise to still get a decent $\epsilon$.

So to take again our example of malware classification, in our previous scheme, each individual teacher would send its vote to the aggregator. Once collected, the repartition of votes would look something like this:

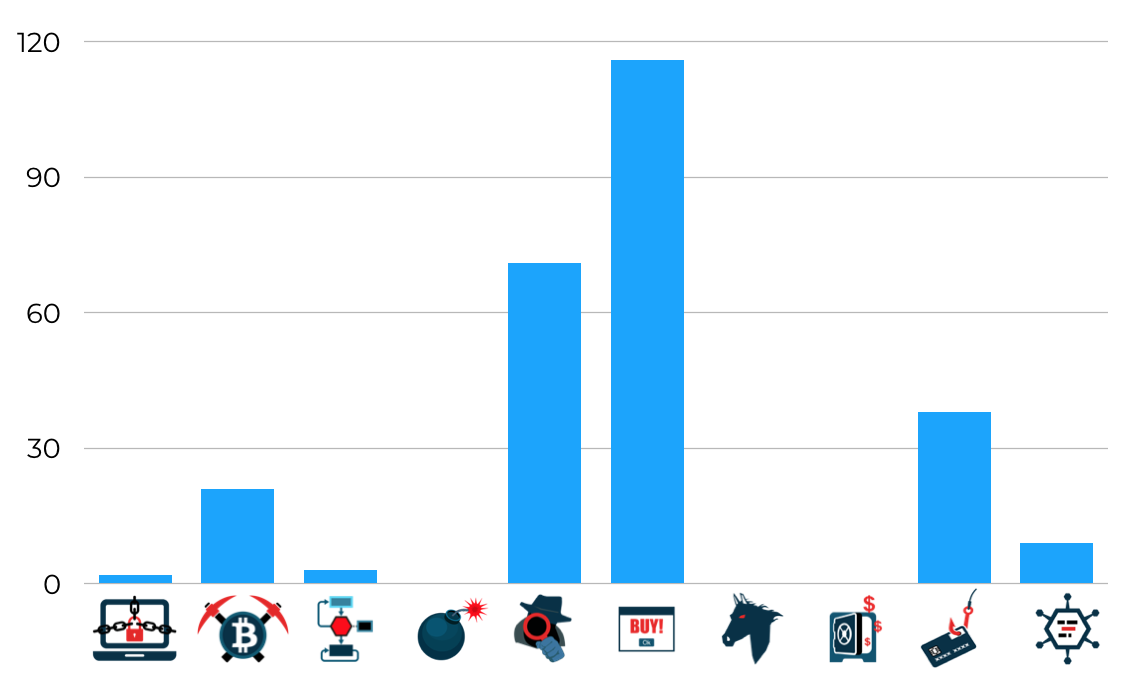
It seems there is a big consensus around class “Adware” even though the class “Spyware” has a non negligeable weight. Teachers also have marginally voted for class “Phishing” and “Miner”. As always, there are also some outliers and “true” noise in these votes, misclassification could happen.

On top of these votes, the aggregator adds some gaussian noise, with appropriate variance $\sigma^2$ to hide the true vote counts per class. The standard deviation $\sigma$ has to be carefully selected and depends on our “privacy budget” $\epsilon$. The new noisy histogram would look something like this:

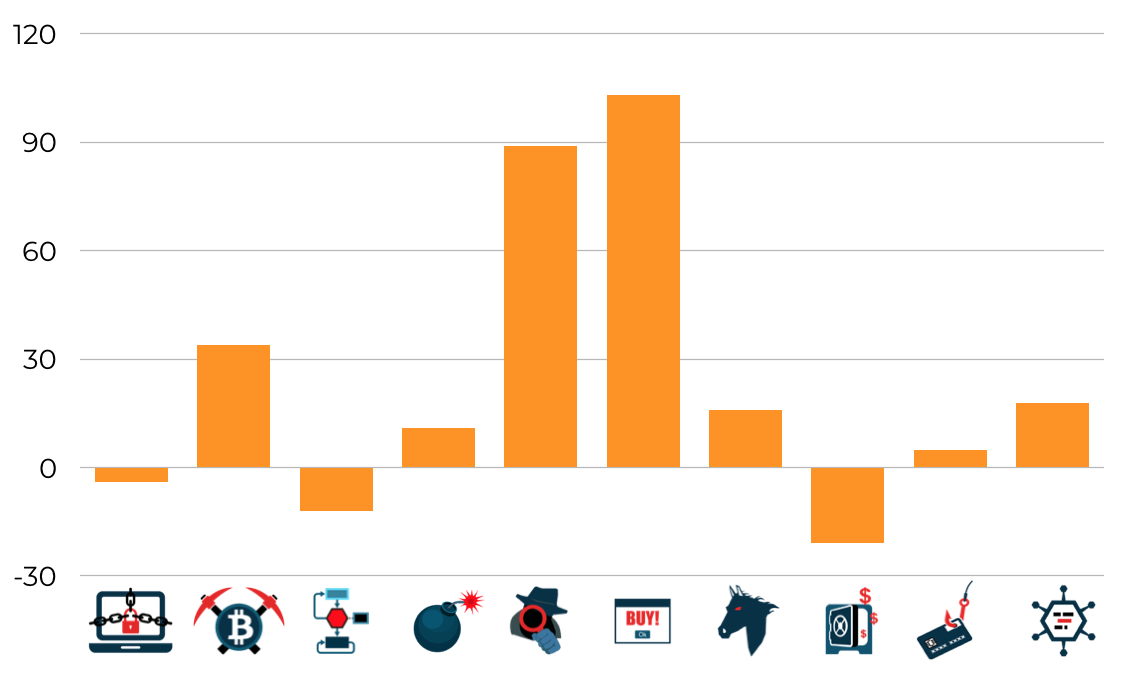
We can see that the noise perturbed a bit the distribution, but kept the order of the two most prominent classes intact (although decreasing a bit the consensus formed around “Adware” and increasing the importance of “Spyware”). Therefore, the assigned label will remain “Adware” in this case.

This is not good enough, as the aggregator learns any individual vote. Indeed, he is responsible for properly noising the votes, and receive them un-noised. A simple workaround would be to allow indeed each client to noise their own vote before sending it to the server / aggregator. Assuming we do want to have a total noise of variance $\sigma^2$, fortunately gaussian random variables add up nicely, and if we have $n$ teachers, we can have each one noising its vote with a gaussian noise of variance $\sigma^2/n$.

However, this typically gives us a noise value so small that it cannot hide the true vote value from the aggregator (see on the graph below, the noised vote still shows a clear peak on the true class value). The final model will indeed be differentially private, it doesn’t change the algorithm, but it doesn’t REALLY respect the “input privacy” problem we talked about earlier.

Un-noised vote	Noised vote • $\mathcal{N}(\mu=0, \sigma = 0.3)$

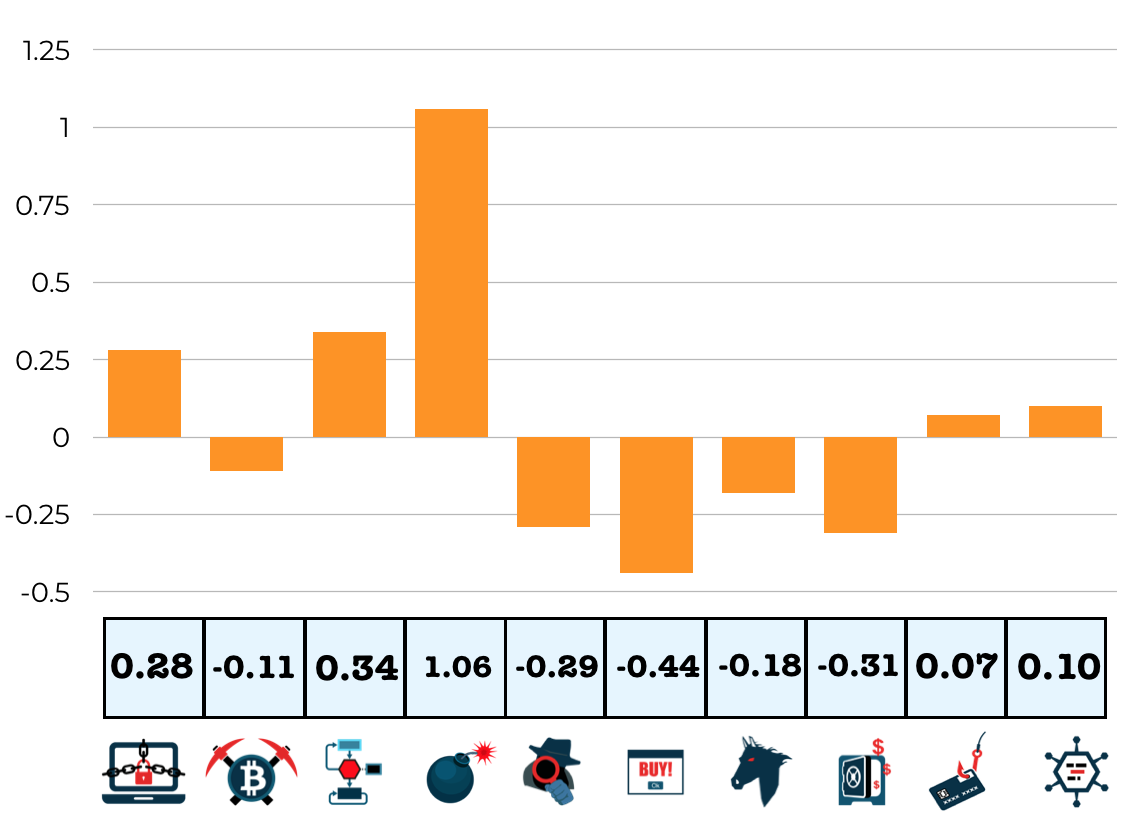Note that the argmax of an individual noised vote vector might not necessarily be representative of the true predicted class of this teacher, but as we sum these votes up, if the teachers agree, a clear majority should emerge anyway.

Also note that one “client” can train multiple teachers. It just had to divide its dataset into $m$ parts, train $m$ teacher models on those disjoint datasets, and aggregate their predictions in one vote vector, before sending it to the server (e.g: [0,0,12,0,0,2,0,1,0,0] for $m = 15$). In the local model, it would noise this vector with a variance equal to $m$ times the variance used to noise a single vote.

So, true input privacy is only guaranteed if we trust a central aggregator. In our example, it could be a server from the Electronic Frontier Foundation, for instance. But in general, having a trusted unpartial server available to perform the aggregation is a very strong assumption.

So, how can we get rid of that trust? This is exactly the sort of question to which Secure Computation has the answer.

Secure Computation

Secure computation is a way to compute a function $y = f(x_1,x_2, …, x_n)$ on $n$ private inputs typically held by $n$ individuals (parties) which does not necessarily trust each other. The output of the computation could be delivered to one or several input parties, or even a distinct individual. The latter should only lean the value $y$, and never learn about these inputs $x_1, x_2, …, x_n$.

To solve our problem of aggregating teachers votes in a secure manner, we can use two different approaches:

• General Secure Multi-Party Computation (MPC) protocols, which allow us to compute any type of function. That way, we will be able to compute the argmax of our noisy sum of votes

• Specific protocols, only tailored for secure aggregation, i.e summing all these private inputs $x_1, x_2, …, x_n$.

So we experimentally design two systems using these two different approaches, suited for two different scenarios:

• In the first scenario, the parties are assumed to be equal in terms of computation power, communication latency, and should be available at all time. There are typically only a few parties, and they are all interconnected in a Mesh architecture.

  In this scenario, we will use a general MPC protocol

• In the second scenario, we assume a lot of non-reliable and weak devices (in terms of computation power), interacting with a central server in a Star architecture. A large portion of these devices can typically drop out during the computation, without affecting the protocol (their input is simply not taken into consideration).

  In this scenario, we will use a secure aggregation protocol

First scenario	Second Scenario

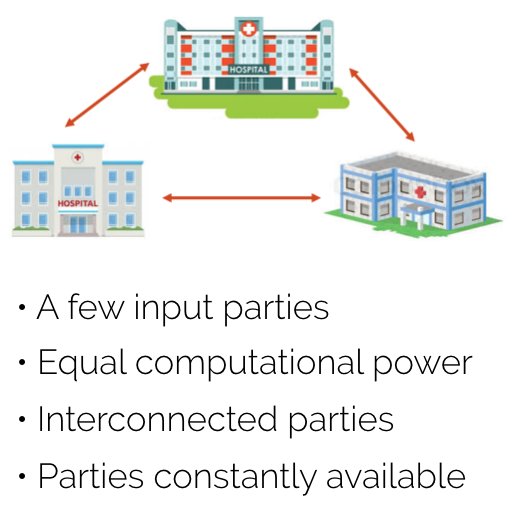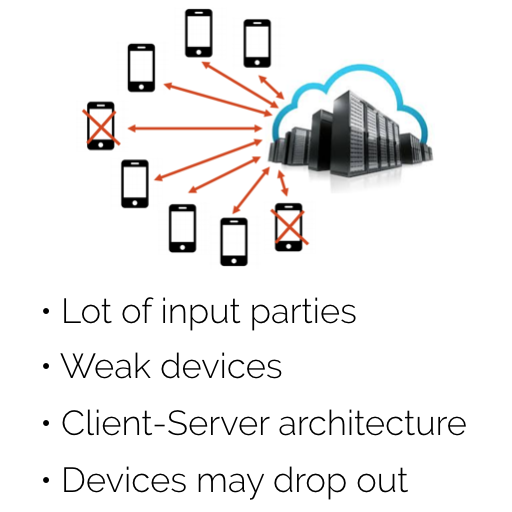Choosing one or the other depends on the use-case. Of course, general MPC is much more expressive, but is typically quite slow and greedy in terms of communication, while the other approach is more suited for a real-world environement and typically offer better performance, but is less adaptable to a system design change.

First scenario - MPYC

For our first scenario, we relied on a General Multiparty Computation scheme based on homorphic secret sharing. We implemented it in Python with the mpyc library, which is based on Shamir secret sharing and Pseudorandom secret sharing.

Secret sharing is a way to split a secret into $n$ different shares and typically distribute these shares to different parties. The secret could be reconstructed out of all (or a portion) of these shares.

The most interesting case is of course when only a portion (a subset) of these shares allow to reconstruct the full secret. This is called t-out-of-n threshold secret sharing (or $(t,n)$ secret sharing). Such a scheme is made of two algorithms:

• $[ \ [![ s ]!]_1, [![ s ]!]_2, …, [![ s ]!]_n ] \leftarrow SS.split(s, t, n)$, which splits our secret $s$ into $n$ shares, from which at least $t$ are needed to reconstruct $s$.
• $s’ \leftarrow SS.recons( [ \ [![ s ]!]_i, [![ s ]!]_j, … ] )$, which reconstructs the original secret $s$ if $| \ [ \ [![ s ]!]_i, [![ s ]!]_j, … ] \ | \geq t$, or outputs any value if not enough shares are provided, or incorrect shares for our secret $s$.

These two algorithms must respect two properties (taken from the book “A Practical Introduction to Secure Multi-Party Computation”):

• Correctness. Let $[ \ [![ s ]!]1, [![ s ]!]2, …, [![ s ]!]n ] \leftarrow SS.split(s, t, n)$. Then: $$ \mathbb{P}[∀k ≥ t, SS.recons( [ \ [![ s ]!]{i_1}, [![ s ]!]{i_2}, …, [![ s ]!]{i_k} ] ) = S] = 1 $$

• Perfect Privacy. Any set of shares of size less than t does not reveal anything about the secret in the information theoretic sense. More formally, for any two secrets $a, b \in D$ and any possible vector of shares $v = [v1, v2, …, vk]$, such that $k < t$ (and $|_k$ denotes appropriate projection on a subspace of k elements): $$ \mathbb{P}[v = SS.split(a)|_{k}] = Pr[v = SS.split(b)|_{k} ] $$

It is not hard to find examples of $(n,n)$ secret sharing (one that creates $n$ shares, and which requires all $n$ shares to reconstruct the secret). Multiplicative secret sharing for instance, needs all shares to be multiplied together to reconstruct the secret. We can also think about how easy it is to simply onion-encrypt a secret $S$ with $n$ keys.

NB: In general, we can create an $(n,n)$ secret sharing scheme by taking any group $G$ with group operation ∗, mapping the shared secret into a group member $S$, selecting $n−1$ random (uniformly distributed) group elements, and publishing the shares $s_1,s_2,…,s_{n-1}$ and the last one, being computed as $s_n = S∗(s_1∗s_2∗…∗s_{n−1})^{−1}$.

In multiplicative secret sharing, we work in the group $\mathbb{Z}_p^*$ (for a prime $p$), and the operation * is the simple mutliplication.

This is information-theorically secure, because anynone in the possession of $n−1$ shares, will still have no information on the shared secret $S$. For each possible value of $S$, there is a possible value of the missing share, and this defines the cardinality of the search space.

The analogy with onion-encryption (although not theorically the same as secret sharing) is exactly what we see in spy movies: The access to the nuclear button is locked with 3 keys, owned by 3 different Russian generals, and it is required to enter the 3 keys at the same time to unlock the mechanism.

Now, what if we only want to require any 2 out of these 3 keys? This would be analogous to (2,3) secret sharing, a 2-out-of-3 scheme. I’m not an expert in padlock mechanism, but I’m sure it exists…

In theory we could build a t-out-of-n from a n,n, but requires a exploding combinatorially many locks and keys.

Building such schemes from a more abstract standpoint requires the problem to be reformulated as an algebraic system of $n$ equations, with $t$ unknowns.

• Shamir’s scheme, relies on polynomial interpolation, where each share is a value $y_i = f(x_i)$ equal to a polynomial of degree $t-1$ evaluated in some points $x_1$, $x_2$, …, $x_n$. Indeed, $d$ distinct points $(x_i, y_i)$ are sufficient to completely determine a polynomial of degree $d-1$ (2 points for a line, 3 points for a quadratic polynomial, etc…), but any subset of

• Blakey’s scheme, relies on geometric considerations to reconstruct the location of a point at the intersection of several hyperplanes, where each share is the equation of an hyperplane. Indeed, in 3 dimensions for instance, 2 surfaces (hyperplanes of dimension 3) would intersect in a line (i.e a hyperplane of dimension 2), and you would need a 3rd hyperplane to reduce further the dimensionality of the intersection to a single point.

• Other schemes, like Mignotte’s or Asmuth-Bloom’s schemes rely on the Chinese Remainder Theorem, where each share is a reduction of the secret modulo some prime numbers.

Our (NAIVE) protocol for $m$ parties + 1 server (which is also a computation party, but only an output party, not an input party) would go as follows:

We want to compute $v = \sum_{i=1}^{m} v_i$

1. Each party $i$ generates shares of its private noisy vote vector $v_i$ (actually just its vote vector, noised with appropriate random Gaussian noise) and distribute one to every other party: $[![ v_i ]!]_1, [![ v_i ]!]_2, …, [![ v_i ]!]_m$

2. Once all the shares are exchanged, without further communication each party $i$ adds its shares of $v_1, v_2, …, v_m$. As the addition operation is homomorphic, they now hold a share of the sum $v$ : $[![ v ]!] = \sum_{j=1}^{m} [![ v_j ]!]_i$.

3. All the parties now send their share of this sum $v$ to the aggregator, which reconstructs it.

4. The aggregator selects the argmax of $v$ as the assigned label.

Note that in the MPC paradigm, every node is a “computation party”, so what we called so far the server or aggregator is an “output party” (i.e receiving an output value), while the other nodes, the clients are “input parties” (i.e contributing an input value).

Following our assumptions of a honest-but-curious setting, clients will respect the protocol (e.g properly noise their input vector), however they will try to learn as much as possible with what is available to them. In particular, clients might want to collude with the server, and share their inputs/outputs.

In this case, they manage to “un-noise” the distribution, by substracting the noise part they generated to the final noisy aggregated sum. Their goal is to learn a closer estimate to the blue histogram above, and break differential privacy.

Hence, we have to design a way for the clients to obliviously send their noise to the server, i.e send a noise value without knowing it. Of course, the server, which will receive it, should neither be aware of this noise value, and aggregate all these noise values together without asking questions.

We can build this system incrementally:

Our first idea is to construct an Oblivious Transfer mechanism, between each client and the server. This means that each client will generate $d$ different noise values (gaussian noise, with same variance), and the server will select 1 out of these $d$, without the client knowing which one.

Without loss of generality, we will choose here $d=2$

Formally, oblivious transfer is defined as follow: A sender $S$ holds 2 private inputs $x_0$ and $x_1$, a receiver $R$ holds a selection bit $b = {0,1}$. The receiver must obtain $x_b$ must not learn any information about $x_{b-1}$. The sender must not learn the value of $b$ (i.e it must not know which of the two inputs was selected).

In our case, we do not require the server to obtain no information about the other (non-selected) noise value, but we absolutely do not want the client to learn which of its inputs was selected by the server. So it is obivious in only one direction. A simple way to implement this protocol is just to send both values to the server, and let it select one.

This is an essential first step, but there is still a catch, since we assumed clients could collude with the server, the latter could communicate which private noise value it selected.

We hence need to design a system in which the server does not even know which value it selected. In other terms, the selection bit $b$ must be oblivious to him.

There is a simple way all parties could come up with a shared list of $m$ random bits (i.e, 1 for each party):

1. We ask each party to generate an array of random bits $r_i$ = [0, 0, 1, 0, 1, …]
2. They secret share it with every other party
3. They XOR their shares of each array $r_1, r_2, …, r_m$ (element-wise)
4. They now hold shares of a final array $r$ which contains random bits, derived with the help of everyone

This array $r$ will contain the selection bits for every party. I.e the server will select the private value $x_{r[j]}$ of party $j+1$ (**NB:** We assumed list indexing started at zero, but our first client has index “1”).

This way, there is no way for the aggregator to recover the un-noised value of the aggregate sum. It would require every client to send their two generated noise values, and then the server would need to try the $2^m$ noise combinations ($d^m$ in the more general case) to remove from the noisy aggregate until eventually finding a combination of values that would give a integer number (i.e the true aggregate value).

Full Protocol: (not CGNMAX)

1. Each party $i$ draws two random gaussian noise values from the same distribution with appropriate variance, and applies it to its vote vector. It obtain two noisy vectors $v_i^0$ and $v_i^1$.

2. Each party secret shares both of these vectors with every other party.

3. Each party derives the shares of this list of selection bits $r$ (NB: They do not recombine their shares and recover the raw list of bits, we want to do the selection under MPC).

4. Each party add the shares of vote vectors they have according to the selection list $r$, i.e, still under MPC they will do $[v] = \sum_{i=1}^m v_i^{r[i-1]}$

5. All the parties now send their share of this sum $v$ to the aggregator, which reconstructs it.

6. The aggregator selects the argmax of $v$ as the assigned label.

TODO: In the CGNMAX one, parties don’t directly noise their votes vector. Each of them generate a noise part, which are aggregated together into a total noise, used to noise the maximum value of the array. If this value passes a certain threshold, we repeat the process of directly noising the votes vectors themselves, and selecting the argmax of the aggregate.

We used mpyc because it efficiently deals with communication (we do not have to reimplement that) and it is in Python, which is easily readable, and understandable by the Machine Learning community (as their language of predilection). They state that this is an academic library, perfect for prototyping.

Each party runs the same code, and they have a “Party ID” pid, so if you want to do a disjonction among parties (as in our case, the distinction between the server (aggregator) and the client), you can branch depending on this pid.

Let’s look at the code:

https://github.com/AlexConnat/MPC-Aggreg/blob/master/main.py

TODO: Explain portion of the code like mpc.input(), mpc.output(), etc… (important functions) -> Already in comments

TODO: Put graph of performances with different number of clients (+Interpolation) and different latency LAN/WAN (explain how we delayed the LAN) + Small Conclusion.

Few Clients	More Clients

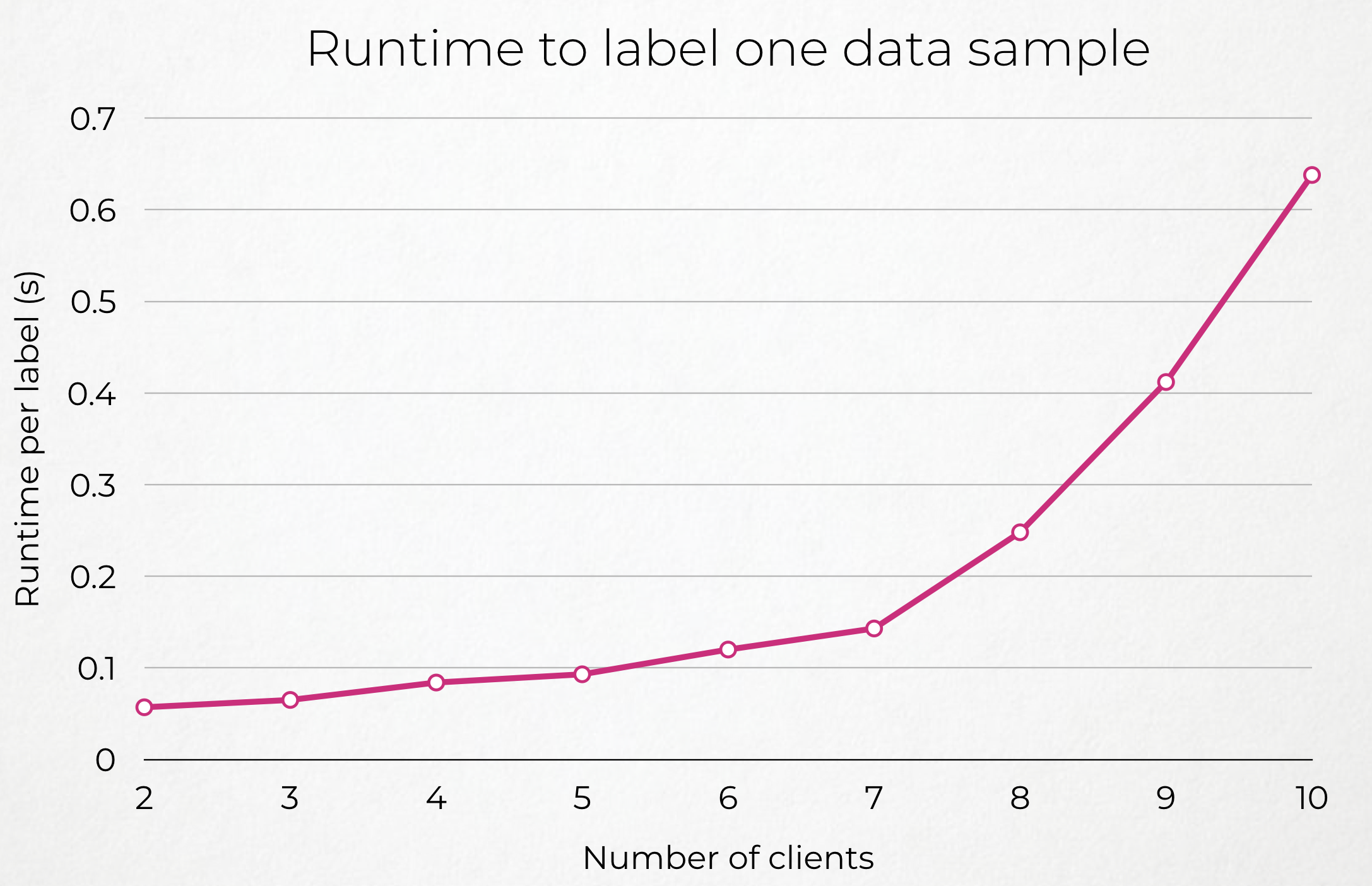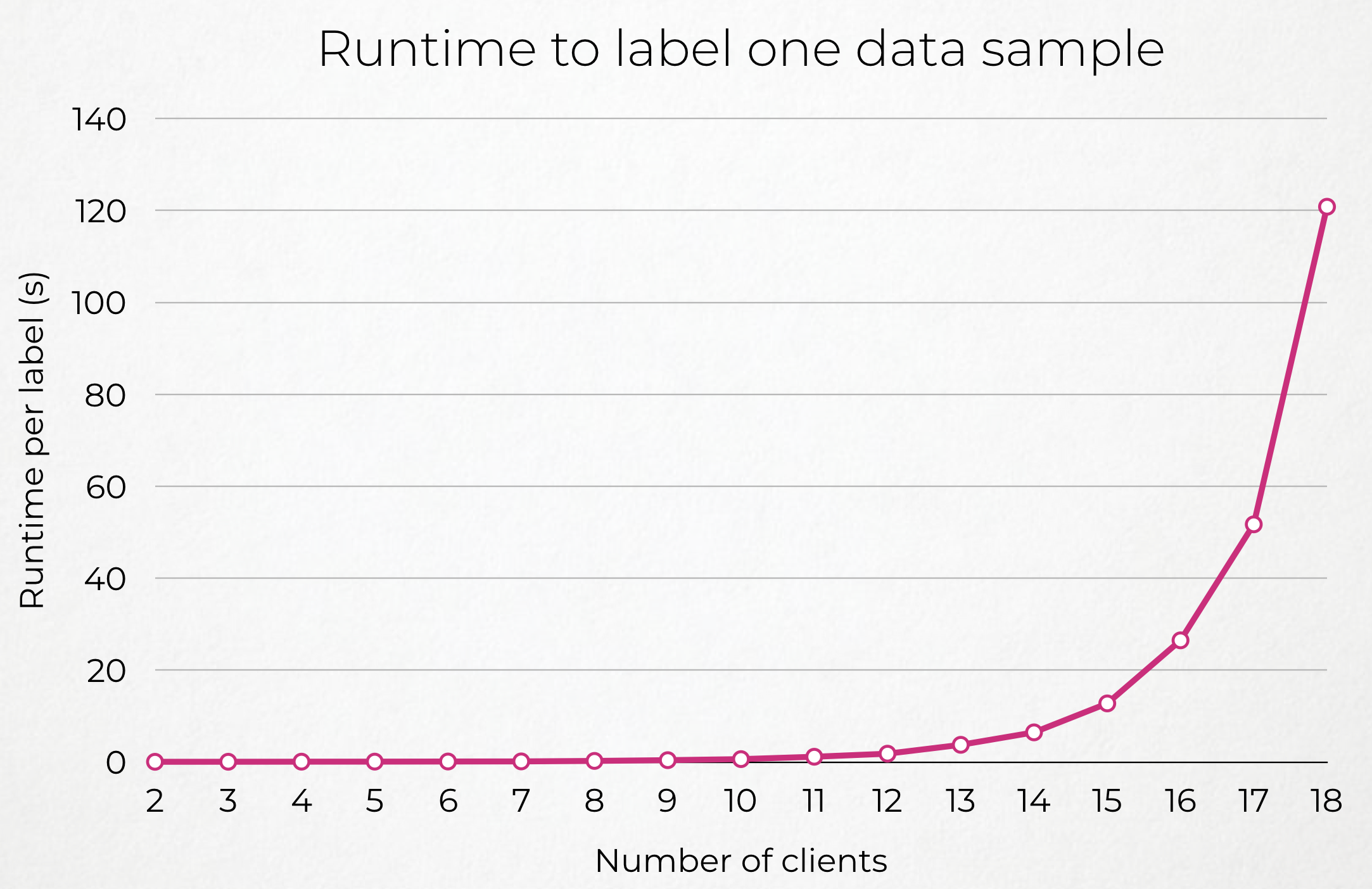Second scenario - SecAgg

For the second scenario, we make use of a protocol by Google, defined in the paper “Practical Secure Aggregation for Privacy-Preserving Machine Learning", that we slightly adapt for our needs.

This protocol uses pairs of self-cancelling blinding vectors to hide the private input of each client, while still getting the correct result when aggregated all together.

The big advantage of this protocol is it can support arbitrary large input vectors, without increasing much performance, and can tolerate up to half of the clients dropping out. However, it is only designed for secure aggregation of vectors, and you cannot for instance perform a secure maximum, or secure argmax on the resulting vector, as with mpyc. The server will eventually learn the full aggregated vector.

To give the intuition behind the protocol, I will take the example of three clients, that could be easily generalized to an arbitrary number of clients.

So we have three clients, each one having its own private input vector $x_i$. For our application, you can imagine these $x_1, x_2, x_3$ as their votes vector. We want to have the server obtain $z = \sum_{}^{} x_i$ without learning any individual $x_i$.

1. All three clients will exchange a “mask” with each other (even though they communicate through encrypted channels, in practice, all messages go though a central server). This mask is simply a vector of same cardinality as the inputs, containing uniformily distributed random values.

   • Client 1 and client 2 will exchange a mask $p_{12}$.
   • Client 1 and client 3 will exchange a mask $p_{13}$.
   • Client 2 and client 3 will exchange a mask $p_{23}$.

2. Clients will mask their input $x_i$ by adding the masks they share with any clients whose ID is higher than theirs (assume a total order on clients IDs) and substract the ones they share with clients with lower IDs. Once masked, they send their output $y_i$ to the server.

   • $y_1 = x_1 + p_{12} + p_{13}$
   • $y_2 = x_2 + p_{23} - p_{12}$
   • $y_3 = x_3 - p_{13} - p_{23}$

3. The server performs a simple summation of the inputs $y_i$ it received from clients, as indeed:
   

$$ \sum_{u=1}^3 y_u = x_1 + \cancel{p_{12}} - \cancel{p_{12}} + x_2 + … = \sum_{u=1}^3 x_u = z $$

However, this protocol, as simple as it could be, has two drawbacks:

• Dropout resistance (+ explain Double Masking, to make it secure against late messages (or lying in the malicious case))
• Communication overhead (-> Explain PRG, and the seed agreed with DHKE)

Indeed, we can observe that the protocol described above is not tolerating any clients dropping out, i.e clients not responding anymore. In our example, what would happen if the second client would crash just after having exchanged masks with every other client? The server would hence receive:

• $y_1 = x_1 + p_{12} + p_{13}$
• $y_2 =$ ???
• $y_3 = x_3 - p_{13} - p_{23}$

The server still want to compute the sum of private inputs of the remaining clients $z’ = x_1 + x_3$, but it cannot just add $y_1 + y_3$ as only the mask $p_{13}$ would cancel out, and the masks shared with the dropped out client ($p_{12}$ and $p_{23}$) would remain in the sum, hence yielding a wrong result.

To solve that problem, during masks derivation and exchange phase, each client should share with every other a 2-out-of-3 secret share of its masks (or a $t$-out-of-$n$, with $t= floor(n/2)+1$ in the general case).

• Client 1 sends to:
  • Client 2: $[![ p_{12} ]!]_2$ and $ [![ p_{13} ]!]_2$
  • Client 3: $[![ p_{12} ]!]_3$ and $ [![ p_{13} ]!]_3$
• Client 2 sends to :
  • Client 1: $[![ p_{12} ]!]_1$ and $ [![ p_{23} ]!]_1$
  • Client 3: $[![ p_{12} ]!]_3$ and $ [![ p_{23} ]!]_3$
• Client 3 sends to:
  • Client 1: $[![ p_{13} ]!]_1$ and $ [![ p_{23} ]!]_1$
  • Client 2: $[![ p_{13} ]!]_2$ and $ [![ p_{23} ]!]_2$

Holding these 2-out-of-3 shares will allow the remaining clients to reconstruct the masks of the ones that dropped out…. ALREADY HAD THEM….. (3 is a bad example). It is to avoid recovery of recovery

With 4, is it 3-out-of-4 or 2-out-of-4 ???

y1 = x1 + p12 + p13 + p14

y2 = x2 + p23 + p34 - p12

y3 = x3 + p34 - p13 - p23

y4 = x4 - p14 - p24 - p34

$x1 + x3 + x4 + \cancel{p13-p13} + \cancel{p14-p14} + \cancel{p34-p34} + p12 + p23 - p24$

If we ask all remaining clients to send shares of masks for p12, p23, p24, as everyone has them, even if a new client drops out during this phase (say y3), we still have 2 shares of p12, 2 shares of p23, two shares of p24 which is enough to reconstruct those masks.

TODO: Write about communication overhead

We modified a bit the protocol so that instead of sending their raw input $x_i$, each client would send a noisy version of their input (i.e, of their vote vector) $\tilde{x}_i$.

What is the amount of noise each client should put?

If we want a total gaussian noise with variance $\sigma^2$, and there are $n$ teachers each teacher prediction should be noised with a variance $\frac{\sigma^2}{n}$. And knowing that a teacher can send the aggregated predictions of $t$ teachers, this vote vector should be noised with variance $\frac{t}{n}\sigma^2$ (i.e a standard deviation of $\sqrt{\frac{t}{n}}\sigma$).

TODO: Explain mechanism to add more noise than needed (in the worst case scenario where half of the nodes drop out), and then remove the noise value of the nodes that didn’t drop out!

TODO: Write about “Multiple teachers per nodes” (not implemented, though) -> Hierarchy of teachers, to get as close as possible to the true variance value.

TODO: Comment the performance graphs (different number of nodes + proportion of nodes dropping out + latency)

TODO: Write a Small Conclusion for the chapter

Few Clients	More Clients

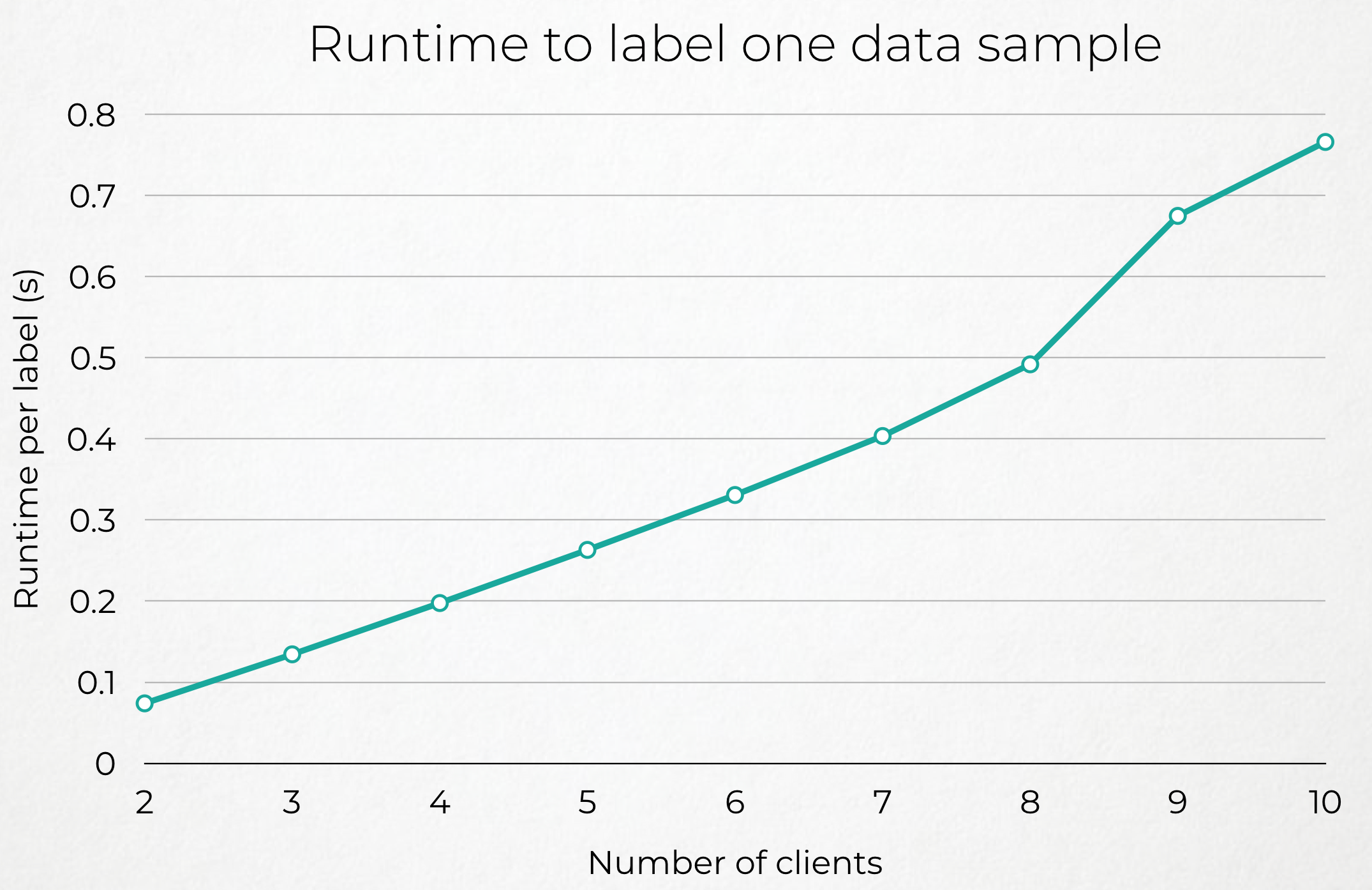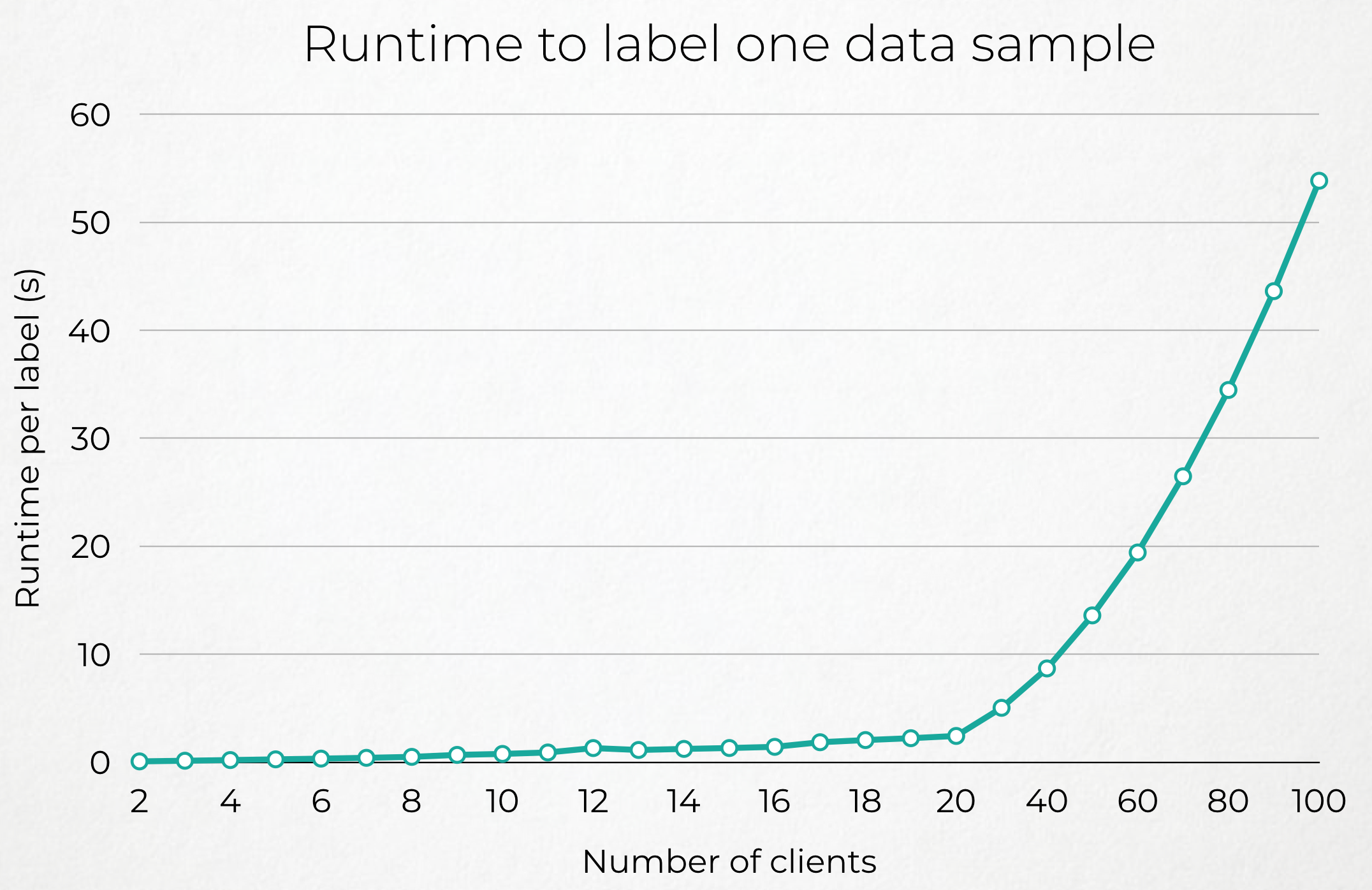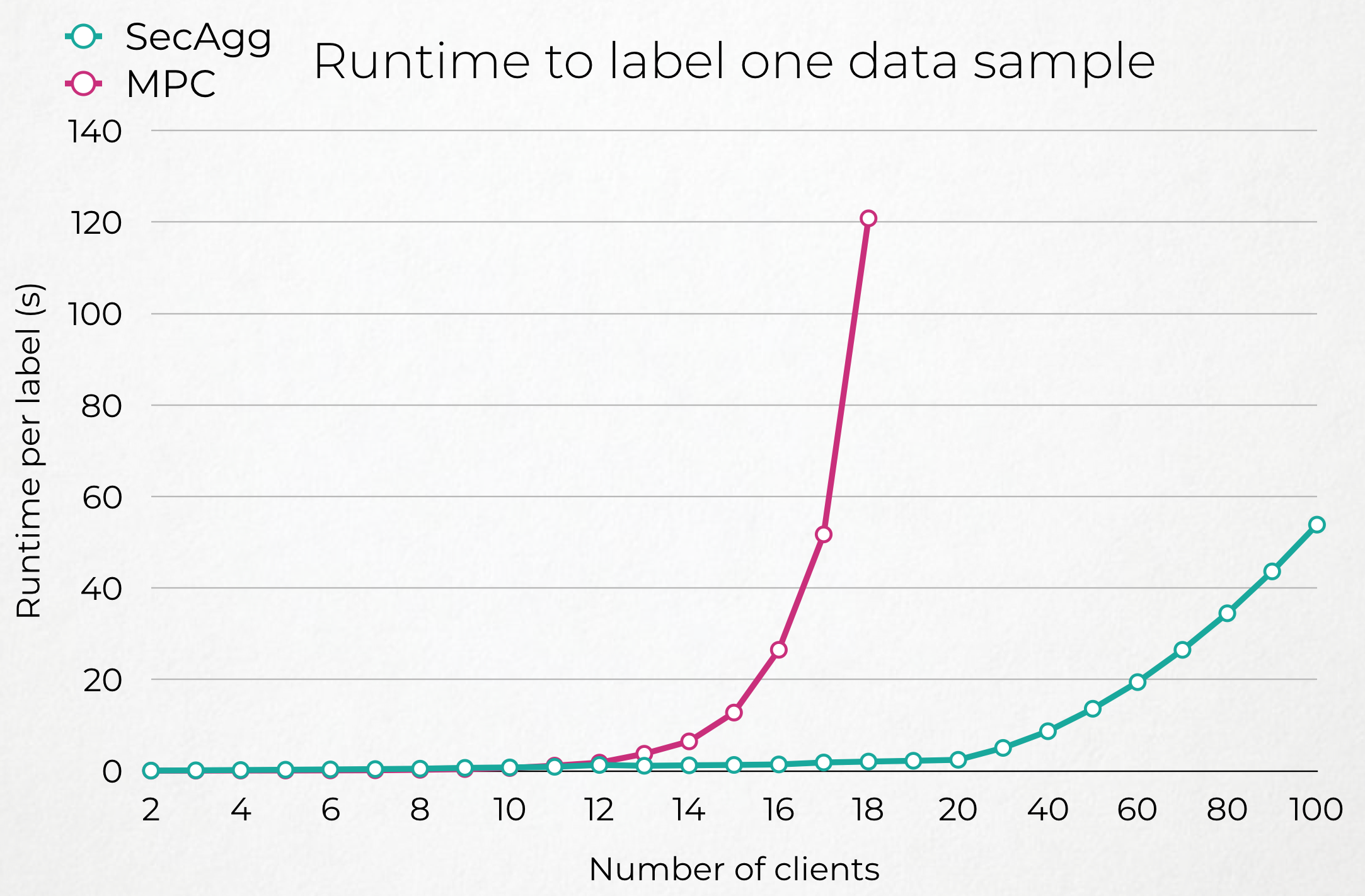
Evaluation

Our evaluation is essentially the time it takes both systems to perform one iteration of the protocol and hence produce one label (or None) for a data sample.

In this part, we do not measure the performance of the actual Machine Learning task, in terms of the accuracy of the student model, as this one depends solely on the amount of noise we introduced in the Knowledge Transfer mechanism. We refer the reader to Table ??? on a summary of these results for the three most common image recognition datasets.

We measured this time on a EC2 AWS Machine m5.4xlarge with 16vCPUs and 64Go of RAM, with a 100GBps ethernet connexion. In our setting, all clients were hosted on the same machine, as different processes. Hence we simulated real latencies introduced by distance between nodes in a LAN or WAN environement using tc.

General Conclusion + Future work

TODO: Compare both implementations, say how this could be further improved, etc…

Few Clients	More Clients

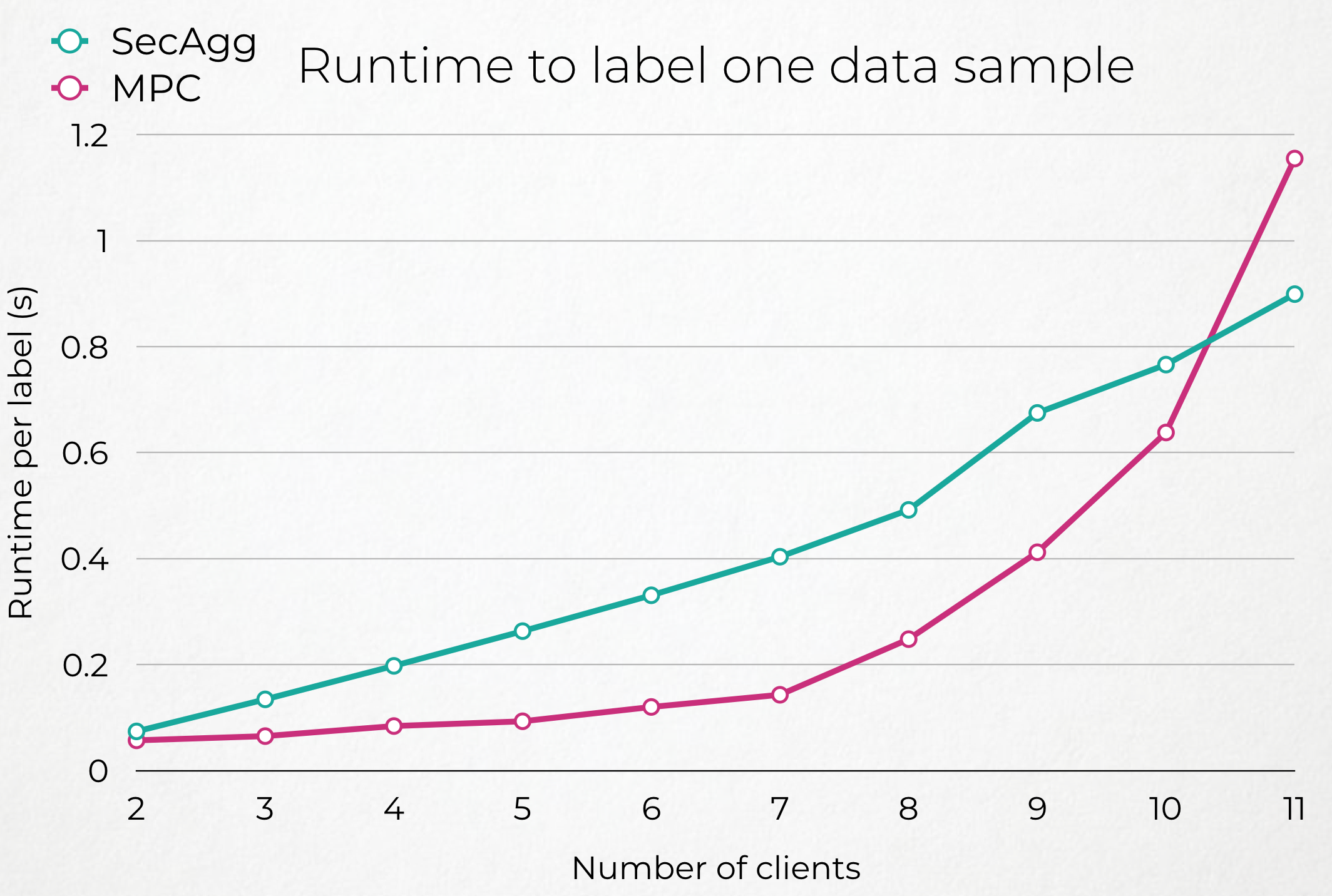TODO: (re-write the “Future Work” section from my Thesis)